DFS

1. 定义

深度优先搜索算法（DFS）是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。

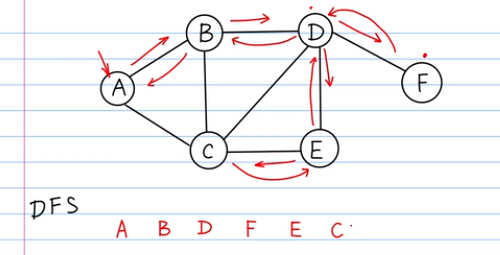
由于在不同节点上选择可以很多种，因此DFS的结果不唯一。

通常使用递归or栈来实现DFS。

2.过程

DFS的过程类似于栈的结构：后进先出，从根节点开始，把处理过的节点弹出栈，把出栈元素的邻接点放入栈中。

（1）A是根节点，A入栈之后出栈，把A的邻接点C、B放进栈。

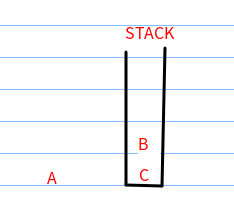
（2）B出栈，B的邻接点D进栈。

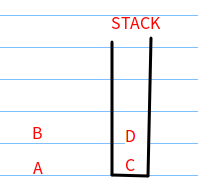
（3）D出栈，E、F进栈。

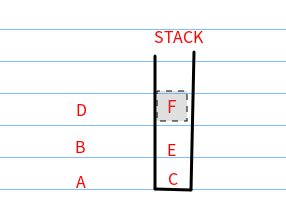
（4）F出栈，发现F没有还没进栈的邻接点。因此把栈里的元素逐一出栈：

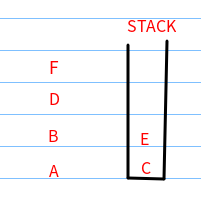
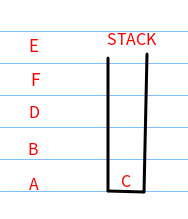
（5）E出栈，最后C出栈。

3. 经典DFS题目

#include <iostream>
#include <cstring>
#include<cstdio>
using namespace std;
#define maxn 30
int w,h,ans;
char arr[maxn][maxn];
int vis[maxn][maxn];


void DFS(int x,int y)
{
    for(int i=0;i<4;i++)
    {
        int dx = x + dir[i][0];
        int dy = y + dir[i][1];
        if(dx>=0 && dy<w && dy>=0 && dx<h && arr[dx][dy]=='.' &&  vis[dx][dy]==0)
        {
            ans++;
            vis[dx][dy] = 1;
            DFS(dx,dy);
        }
    }
}
int main()
{
    while(scanf("%d %d",&w,&h) && (w+h))
    {
        ans =0;
        for(int i=0;i<h;i++)
        {
            scanf("%s",arr[i]);
        }
        memset(vis,0,sizeof(vis));
        for(int i=0;i<h;i++)
        {
            for(int j=0;j<w;j++)
            {
                if(arr[i][j]=='@')
                {
                    vis[i][j]=1;
                    ans++;
                    DFS(i,j);
                }
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}

（2）类八皇后问题+DFS

HDU 1045 Fire Net

题目大致意思是，有一个最多4*4列的棋盘，’.‘表示可走，但子弹不能出现在同一列，同一行，同一斜对角。’X’表示墙，子弹不能穿过墙，即隔着墙的子弹能在同行同列或者斜对角，求最多能有多少个子弹穿过棋盘。

#include <iostream>
#include <stdio.h>
#include <cmath>
#include <algorithm>
using namespace std;
char map[5][5];
int vis[5][5];
int maxx;
int n;
int judge(int xx,int yy)  //判断该坐标是否能走（是否有墙或障碍）
{
    int i;
    for(i=xx;i>=0;i--)
    {
        if(vis[i][yy]==1)  //已经走过的行
            return 0;
        if(map[i][yy] == 'X')  //有障碍不能走
            break;
    }
    for(i=yy;i>=0;i--)
    {
        if(vis[xx][i] == 1)
            return 0;
        if(map[xx][i] == 'X')
            break;
    }
    return 1;
}
void dfs(int num,int cnt)  //num是当前搜索到的点，cnt是计算能走棋盘的子弹数量
{
    //递归出口
    if(num == n*n)
    {
        maxx = max(maxx,cnt);
        return;
    }
    //获取下标
    int x = num/n;  //坐标搜索如下图
    int y = num%n;
    if(map[x][y] == '.' && judge(x,y))  //判断该地方是可行,并且没有炮台
    {
        vis[x][y] = 1;
        dfs(num+1,cnt+1);
        vis[x][y] = 0;
    }
    dfs(num+1,cnt);//若不满足if（子弹不能走），则下一个坐标搜索

}
int main()
{
    while(scanf("%d",&n)!=EOF && n)
    {

         maxx = 0;
         for(int i=0;i<n;i++)
         {
            scanf("%s",map[i]);
         }
         dfs(0,0); //从0的位置开始搜索，开始时0个子弹
        cout << maxx << endl;
    }
}

棋盘搜索方向：

1. 定义

2.过程

3. 经典DFS题目

FEATURED TAGS

FRIENDS