数据结构

BFS

Posted by Liao on 2019-08-31

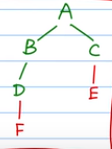
1. 定义

​ 树的BFS：从根节点开始，从左到右，从上到下进行的层次遍历；

​ 图的BFS：从根节点出发，找与该结点相邻的所有结点，如此类推，一层层遍历。

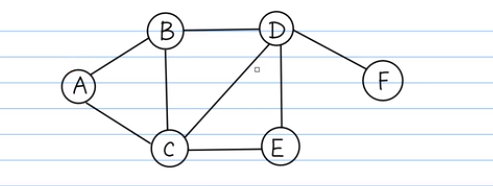
​ 图没有根结点，就得找一个点作为根节点。例如是A，则找与A相连距离1条边的结点，有B、C；再找与A距离2条边的结点有D、E；最后与A距离为3的结点有F。故BFS的遍历顺序为：ABCDEF

注意，取的点不同，有不同的遍历结果。例如遍历A结点之后，遍历B、C，则第三层要把与B相连的所有邻接点遍历完，即是ABCDE,而不能是ABCED，因为E结点和B没有直接相连。

另外一种遍历方式也可以是：ACBEDF 。

2. BFS用队列保证层的顺序

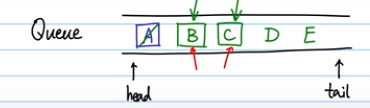
​ 队列是先进先出的特点，把BFS遍历的结点从队尾开始进入，再从队头出来。每出队一个元素，则把该元素的所有邻接点入队，以保证层的顺序。

例如先把A结点入队，A出队的时候把A所有邻接点入队，即B、C，由于B在C的前面，B的邻接点要比C的邻接点先出现，故把D塞进来，再到E。如此类推。（保证了先进来的B、C离A比较近，后进来的离A较远）

3.例题

给出一个二维数组，每次只能走该点的上下左右，且每次只能走从高到低的点，没走过一个点距离+1。问走的最大距离是多少。

5 4
1 2 3 4
16 17 18 5
15 29 25 6
14 11 22 7
23 10 9 8

输出最大距离为18

25->18->17->16->15->14->11->10->9->8->7->6->5->4->3->2->1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include <iostream>
#include <cstring>
using namespace std;
const int maxn = 1e2 + 10;
int Map[maxn][maxn];
int dp[maxn][maxn];
int row,col;

int check(int i,int j)
{
    return (i >= 1 && j >= 1 && i <= row && j <= col);
}

int BFS(int i,int j)
{
    int Max = 0;
    if(check(i,j+1)  && Map[i][j] > Map[i][j+1])  //向右广搜  满足搜索的点比现在的点小
    {
        if(dp[i][j+1])  //如果这个点走过
            Max = Max > dp[i][j+1] ? Max : dp[i][j+1];  //如果走过，则比较现在的点长还是之前的点长
        else
            Max = Max > BFS(i,j+1) ? Max : BFS(i,j+1);
    }

    //向下广搜
    if(check(i+1,j) && Map[i][j] > Map[i+1][j])
    {
        if(dp[i+1][j])
            Max = Max > dp[i+1][j] ? Max : dp[i+1][j];
        else
            Max = Max > BFS(i+1,j) ? Max : BFS(i+1,j);
    }

    //向左广搜
    if(check(i,j-1) && Map[i][j] > Map[i][j-1])
    {
        if(dp[i][j-1])
            Max = Max > dp[i][j-1] ? Max : dp[i][j-1];
        else
            Max = Max > BFS(i,j-1) ? Max : BFS(i,j-1);
    }

    //向上广搜
    if(check(i-1,j) && Map[i][j] > Map[i-1][j])
    {
        if(dp[i-1][j])
            Max = Max > dp[i-1][j] ? Max : dp[i-1][j];
        else
            Max = Max > Map[i-1][j] ? Max : BFS(i-1,j);
    }


    if(Max == 0)
        dp[i][j] = 1;
    else
        dp[i][j] = Max + 1;

    return dp[i][j];
}

int main()
{
    while(cin >> row >> col)
    {
        memset(dp,0,sizeof(dp));
        for(int i = 1; i<=row; i++)
            for(int j = 1; j<=col; j++)
                cin >> Map[i][j];
        int ans = 0;
        for(int i=1;i<=row;i++)
        {
            for(int j=1;j<=col;j++)
            {
                int tmp = BFS(i,j);
                if(tmp > ans)
                    ans = tmp;
            }
        }

        cout << ans <<endl;
    }
    return 0;

}



LeetCode 腐烂的橘子

在给定的网格中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。
每分钟，任何与腐烂的橘子（在 4 个正方向上）相邻的新鲜橘子都会腐烂。

返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1。

代码中~dis[tx][ty]是位运算中的取反，二维数组dis开始初始化为-1，-1取反为0，此处就是判断dis[tx][ty]是否为0，根据题意，0就是没有橘子的地方，不作处理。

队列用来存放腐烂橘子的坐标，能把该坐标上下左右新鲜的橘子变腐烂。

make_pair(i,j) 无需写类型就能生成pair对象，可以直接放入队列中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
int orangesRotting(vector<vector<int>>& grid) {
       int cnt = 0,ans = 0;
       int dis[10][10];
       int dir_x[4] = {1,0,-1,0};  //右下左上四个方向的坐标
       int dir_y[4] = {0,-1,0,1};
       queue<pair<int,int>> q;
       memset(dis,-1,sizeof(dis));  //数组初始化
       int n = grid.size(), m = grid[0].size();  //行 列
       for(int i = 0; i < n; i++){
           for(int j = 0; j < m; j++){
               if(grid[i][j] == 2){
                   q.push(make_pair(i,j));  //找出最先腐烂句子的坐标，放进队列中。
                   dis[i][j] = 0;
               }
               else if(grid[i][j] == 1)
                   cnt++;
           }
       }

       while(!q.empty()){
           pair<int,int> x = q.front();
           q.pop();
           for(int i = 0; i < 4; i++){
               int tx = x.first + dir_x[i];
               int ty = x.second + dir_y[i];
          
             	if(tx < 0 || tx >= n || ty < 0 || ty >= m || ~dis[tx][ty] || !grid[tx][ty])
                   continue;
               dis[tx][ty] = dis[x.first][x.second] + 1;  //腐烂橘子的下一个 也是腐烂橘子
               q.push(make_pair(tx,ty));  //把新腐烂的橘子放到队列处理

               if(grid[tx][ty] == 1)
               {
                   cnt--;
                   ans = dis[tx][ty];
                   if(!cnt)
                       break;
               }
           }
       }
       return cnt ? -1 : ans;  // 判断cnt是否为0，若是返回ans；不是则返回-1，表示还有1（新鲜的橘子）
   }

LeetCode 地图分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
int maxDistance(vector<vector<int>>& grid) {
    int dir_x[4] = {0,1,0,-1};
    int dir_y[4] = {1,0,-1,0};
    queue<pair<int,int>>q;
    int n = grid.size();
    int m = grid[0].size();
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            if(grid[i][j] == 1){
                q.push(make_pair(i,j));  //把陆地的坐标存入队列;
            }  
        }
    }
    if(q.empty() || q.size() == n*m)  //全是海洋或者全是陆地
        return -1;
   
    pair<int,int>x;
    while(!q.empty()){
        x = q.front();
        q.pop();
        for(int i = 0; i < 4; i++){
            int tx = x.first + dir_x[i];
            int ty = x.second + dir_y[i];
            if(tx < 0 || tx >= n || ty < 0 || ty >= m || grid[tx][ty] != 0)
                continue;
            grid[tx][ty] = grid[x.first][x.second] + 1;
            q.push(make_pair(tx,ty));
        }
    }
    return grid[x.first][x.second] - 1;

}
FEATURED TAGS
数据结构
FRIENDS