红黑树(Red Black Tree)是对二叉搜索树的改进,解决二叉搜索树多次插入新节点导致的不平衡问题。对于搜索、插入和删除较多操作的情况下,通常使用红黑树。
红黑树的底层结构是二叉查找树。
其产生过程:链表->二叉树->二叉查找树->自平衡的二叉查找树
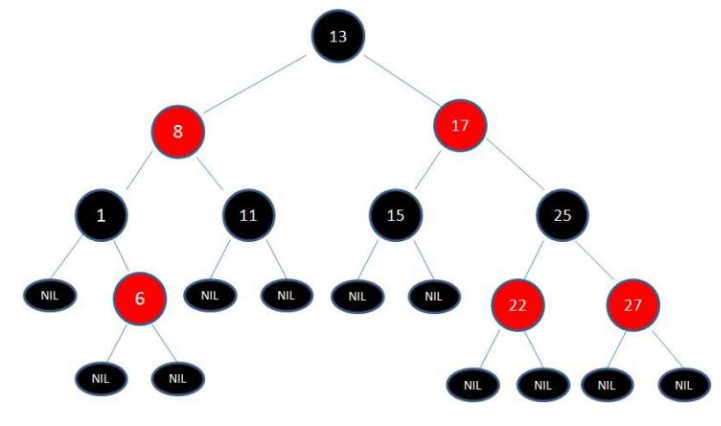
特性
以下特性保证了红黑树的平衡特性,确保没有一条路径比其它路径长出两倍
- 是自平衡的二叉查找树
- 结点是红色或黑色
- 根节点(没有入度或者没有父节点)是黑色的
- 每个叶子节点都是黑色的空结点(NIL结点)
- 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
插入
旋转和变色规则:所有插入的点默认是红色
1) 变色
红变黑,黑变红。
什么时候变颜色呢?举个栗子插入6:
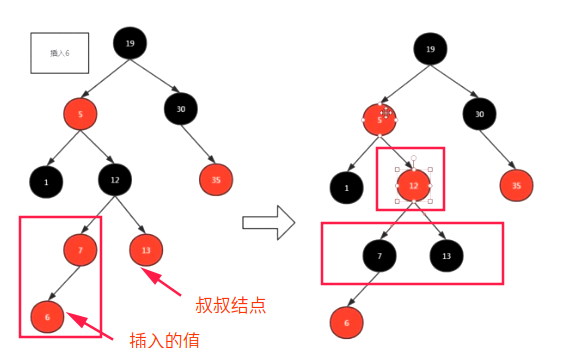
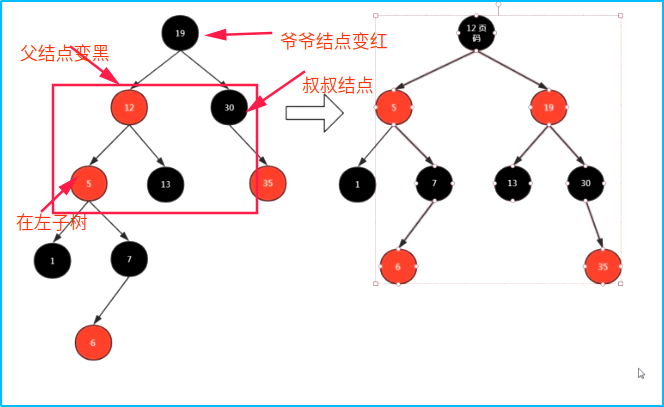
由于二叉查找树的性质,结点6要插在这里。这时,6的父结点也是红色,其叔叔结点也是红色,则把父节点和叔叔结点变黑,并把爷爷结点变红。
2) 左旋
左旋的情况:父结点是红色,叔叔结点是黑色,并且当前结点在右子树上。
左旋的过程:
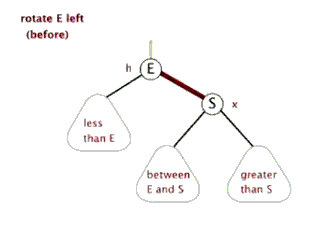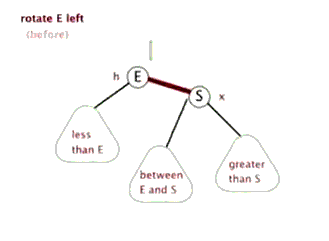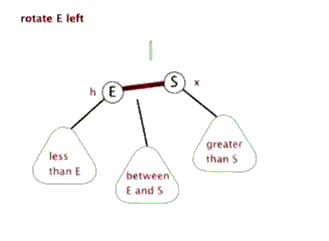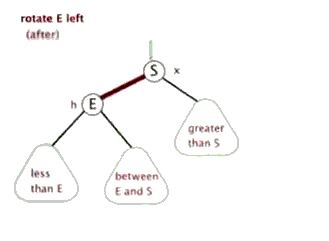
接着上面的情况,变完色之后:
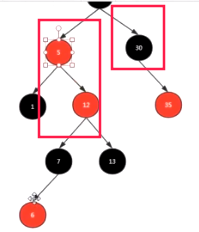 ——>
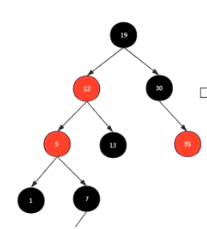
——>
3) 右旋
右旋的情况:父结点是红色,叔叔结点是黑色,并且当前结点在左子树上。
要把父结点变为黑色,把爷爷结点变为红色,再进行右旋。
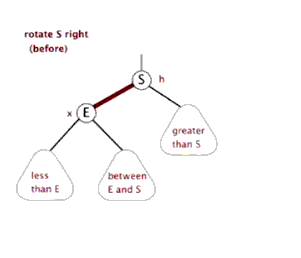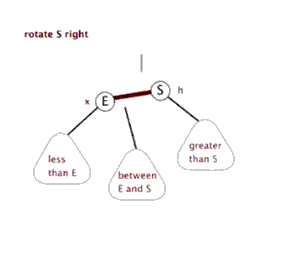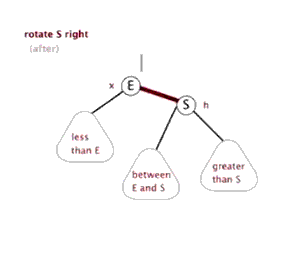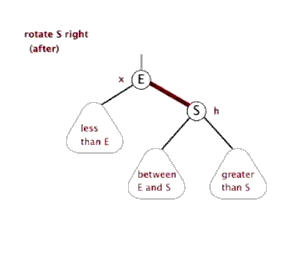
接着上述情况:
实际应用
它是内存查找高效的树(底层系统做内存运算)。
但不适合大数据量,也不适合磁盘存储,其树的深度会很大,会造成IO浪费以及读取资源浪费。