树状数组

对于长度为n的数组进行修改和查询

如果对1~m个数进行求前缀和，复杂度为O(n)。如果n很大效率会非常低。而树状数组只用O(logn)

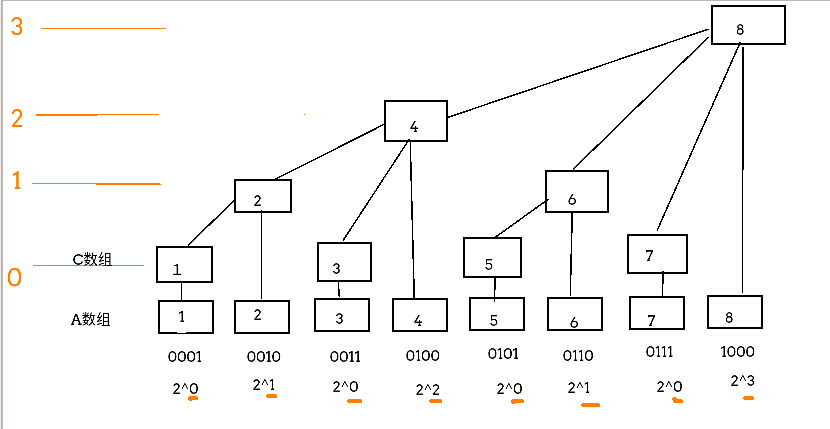
A是原数组，C是新开辟的数组，C[i]的意思是求前**lowbit(i)**个元素的前缀和，同时也是下标i管辖的元素个数2^k，k是i二进制末尾0的个数

例如C[8] lowbit(8) = 1000 & 1000 = 1

| 8-1 = 7

      lowbit(7) = 111 & 001 = 001

| 7-1=6

lowbit(6) = 110 & 010 = 010

| 6-2=4

lowbit(4) = 100 & 100 = 100

| 4-4=0

数组下标的数字转换为二进制后，2^n其中n表示倒数一个1后有多少个0。根据规律能对应树的层，从而画出这个树状数组C[]

C[1] = A[1]

C[2] = A[1]+A[2]

C[3] = A[3]

C[4] = C[2] + C[3] + A[4]= A[1] + A[2] + A[3] + A[4]

C[5] = A[5]

C[6] = C[5] + A[6] = A[5] + A[6]

C[7] = A[7]

C[8] = C[4] + C[6] + C[7] + A[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8]

由此可得，求前缀和时能减少一些运算

lowbit

lowbit()的作用是求二进制数的最低位1的位置在哪。例如lowbit(6)，6的二进制为110，-6为二进制的取反加010，110 & 010 = 010，所以最低位1在第2位。

1
2
3

int lowbit(int n){
    return n & (-n);
}

查询

int getsum(int x)
{
    int i;
    int temp=0;
    for(i=x;i>=1;i-=lowbit(i))
    {
        temp+=c[i];
    }
    return temp;
}

修改

修改操作和查询相反，

void update(int t,int value)
{
    int i;
    for(i=t;i<=n;i+=lowbit(i))
    {
        c[i]+=value;
    }
}

树状数组＋离散化解决逆序对

离散化

先对输入的数组离散化，使得各个元素比较接近，而不是离散的

例如a[9,1,0,5,4]

{v=9, ord = 1} 按照v的大小排序后：　 {v=0, ord = 3}

{v=1, ord = 2} —————————>　　　　 {v=1, ord = 2}

{v=0, ord = 3} —————————> {v=4, ord = 5}

{v=5, ord = 4} —————————> {v=5 ord = 4}

{v=4, ord = 5} —————————> {v=9, ord = 1}

aa[p[i].ord] = i

故有

a[p[1].3] = 1 a[3] = 1

a[p[2].2] = 2 a[2] = 2

a[p[3].5] = 3 a[5] = 3

a[p[4].4] = 4 a[4] = 4

a[p[5].1] = 5 a[1] = 5

aa[5] = {5,2,1,4,3}

struct Node{
    int v; //原输入的值
    int ord;　//下标
}p[510000];
int a[510000];// 原来的数组

for(int i = 1; i <= n; i++){  //n是数组大小
    aa[p[i].ord] = i;  //aa是离散化后的数组
}

参考

树状数组入门

离散化

lowbit

查询

修改

树状数组＋离散化解决逆序对

离散化

FEATURED TAGS

FRIENDS