图论

拓扑排序

Posted by Liao on 2020-05-17

拓扑排序是用于处理一连串的事情，这些事情之间有顺序或依赖关系，在做一件事情之前必须做另一件先（如课程表）

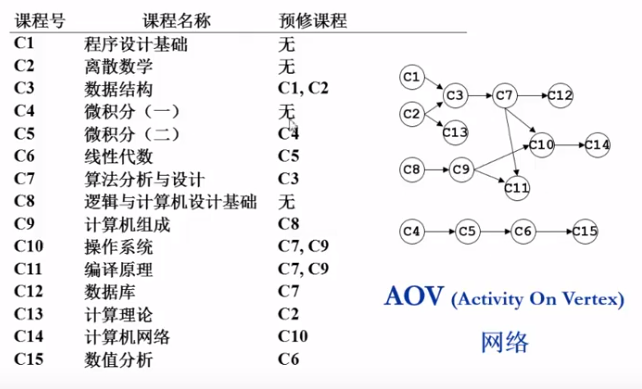
拓扑序：如从图中v到w有一条有向路径，则v一定排在w之前。满足此条件的顶点序列就是一个拓扑序。

拓扑排序：获得一个拓扑序的过程就是拓扑排序。

AOV如果是合理的(不带环)拓扑序，则必定是有向无环图 (Directed Acyclic Graph,DAG)

图的出度和入度体现了顶点的先后关系，入度为0表示说明它是起点，在最前面。出度为0说明它排在最后面。

LeetCode　课程表

样例2的拓扑图如下：

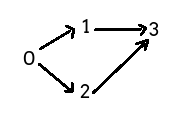
1589688597734

edge[0] = {1,2} indeg[1]++ indeg[2]++

edge[1] ={3} indeg[3]++

edge[2] = {3} indeg[3]++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>>edges;　//存储有向无环图
        vector<int>indeg; //存储入度
        vector<int>result;　//存储结果
        edges.resize(numCourses);
        indeg.resize(numCourses);
        for(vector<int>info : prerequisites){
            edges[info[1]].push_back(info[0]); //存储有向无环图[1,0]要学1得先学0
            ++indeg[info[0]];//入度增加
        }
        queue<int>q;
        for(int i = 0; i < numCourses; i++){
            if(indeg[i] == 0){ //这个点入度为0，就是排在前面，则放入队列
                q.push(i);
            }
        }
        while(!q.empty()){
            int u = q.front();
            q.pop();
            result.push_back(u);
            for(int v : edges[u]){  //v可以代表某个edge集合中的顶点
                --indeg[v]; //集合中某个顶点的度-１
                if(indeg[v] == 0){ //度为0，表示在最前面，则入队处理
                    q.push(v);
                }
            }
        }
        if(result.size() != numCourses) //出现环
            return {};
        return result;
    }
};
FEATURED TAGS
图论
FRIENDS