字符串

字符串和位运算的应用

Posted by Liao on 2023-01-18

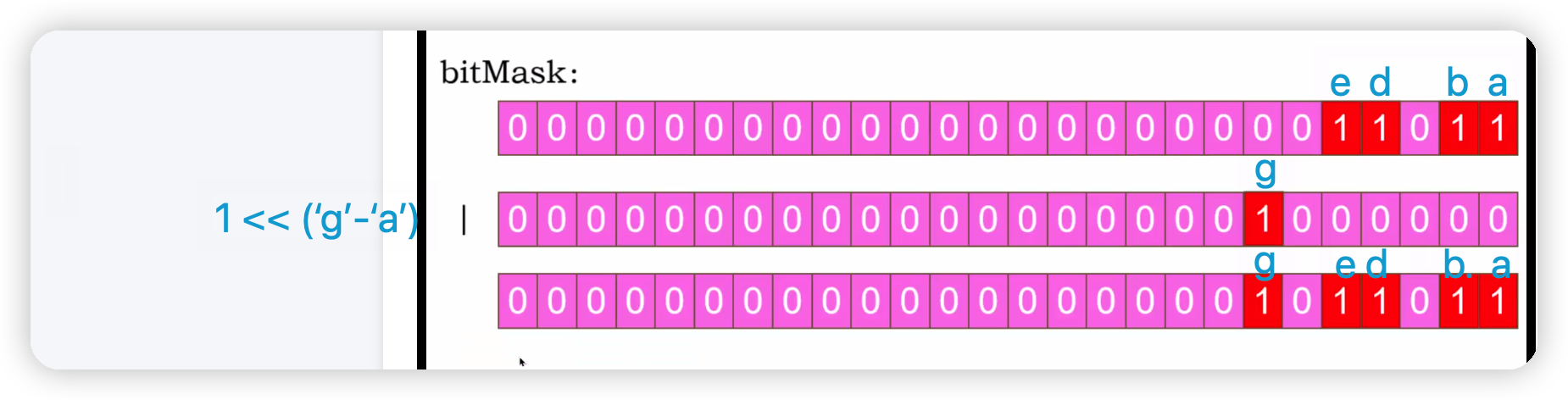
判断字符串是否由相同字符组成，可以结合位运算来计算，提升效率。

一、原理

1、对字符串每个单词进行位运算

1
2
3
4
5
// word1 = "abdeg" 
  int bitmask1 = 0; bitmask = 0;
  for(char c : word1) {
    mask1 |= 1 << (c - 'a');
  }

2、根据各自 | 运算得出来的结果，进行 & 运算，若结果不是0的，即是有相同字符的字符串。

1
2
3
4
5
6
7
8
9
10
11
12
13

bool hasSameChar(string word1, string word2) {
  int bitmask1 = 0; bitmask = 0;
  for(char c : word1) {
    mask1 |= 1 << (c - 'a');
  }
  
   for(char c : word2) {
    mask2 |= 1 << (c - 'a');
  }
  
  return (mask1 & mask2) != 0;
}

二、例题

LC周赛2506. 统计相似字符串对的数目

给你一个下标从 0 开始的字符串数组 words 。

如果两个字符串由相同的字符组成，则认为这两个字符串 相似 。

  • 例如，"abca" 和 "cba" 相似，因为它们都由字符 'a'、'b'、'c' 组成。
  • 然而，"abacba" 和 "bcfd" 不相似，因为它们不是相同字符组成的。

请你找出满足字符串 words[i] 和 words[j] 相似的下标对 (i, j) ，并返回下标对的数目，其中 0 <= i < j <= word.length - 1 。

示例 1：

1
2
3
4
5
输入：words = ["aba","aabb","abcd","bac","aabc"]
输出：2
解释：共有 2 对满足条件：
- i = 0 且 j = 1 ：words[0] 和 words[1] 只由字符 'a' 和 'b' 组成。 
- i = 3 且 j = 4 ：words[3] 和 words[4] 只由字符 'a'、'b' 和 'c' 。
1
2
3
4
5
6
7
8
9
10
11
12
13
int similarPairs(vector<string>& words) {
    unordered_map<int, int>mp;
    int cnt = 0;
    for(string word : words) {
        int mask = 0;
        for(char c : word) {
            mask |= 1 << (c - 'a');
        }
        cnt += mp[mask];
        mp[mask]++;
    }
    return cnt;
}
剑指 Offer II 005. 单词长度的最大乘积

给定一个字符串数组 words，请计算当两个字符串 words[i] 和 words[j] 不包含相同字符时，它们长度的乘积的最大值。假设字符串中只包含英语的小写字母。如果没有不包含相同字符的一对字符串，返回 0。

示例 1:

1
2
3
输入: words = ["abcw","baz","foo","bar","fxyz","abcdef"]
输出: 16 
解释: 这两个单词为 "abcw", "fxyz"。它们不包含相同字符，且长度的乘积最大。

预计算 + 位运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
int maxProduct(vector<string>& words) {
    int n = words.size();
    unordered_map<int, int>mp; // key单词的掩码，val长度
    
    //预处理字符是否有相同，保存在mp中。
    for(int i = 0; i < n; i++) {
        int bitmask = 0;
        for(char c : words[i]) {
            bitmask |= 1 << (c - 'a');
        }
        if(mp.count(bitmask)) {
            int maxval = max(mp[bitmask], (int)words[i].size());
            mp[bitmask] = maxval;
        }
        else {
            mp[bitmask] = words[i].size();
        }
    }

    int ans = 0;
    for(auto& x : mp) {
        for(auto& y : mp) {
          // 虽然需要2次循环，
          // 但通过map存储起每个单词的最大的长度，
          // 减少了多次重复的计算
            if((x.first & y.first) == 0) { 
                ans = max(x.second * y.second, ans);
            }
        }
    }
    return ans;
}
LC周赛2564. 子字符串异或查询

给你一个 二进制字符串 s 和一个整数数组 queries ，其中 queries[i] = [firsti, secondi] 。

对于第 i 个查询，找到 s 的 最短子字符串 ，它对应的 十进制值 val 与 firsti 按位异或 得到 secondi ，换言之，val ^ firsti == secondi 。

第 i 个查询的答案是子字符串 [lefti, righti] 的两个端点（下标从 0 开始），如果不存在这样的子字符串，则答案为 [-1, -1] 。如果有多个答案，请你选择 lefti 最小的一个。

请你返回一个数组 ans ，其中 ans[i] = [lefti, righti] 是第 i 个查询的答案。

子字符串 是一个字符串中一段连续非空的字符序列。

示例 1：

1
2
3
输入：s = "101101", queries = [[0,5],[1,2]]
输出：[[0,2],[2,3]]
解释：第一个查询，端点为 [0,2] 的子字符串为 "101" ，对应十进制数字 5 ，且 5 ^ 0 = 5 ，所以第一个查询的答案为 [0,2]。第二个查询中，端点为 [2,3] 的子字符串为 "11" ，对应十进制数字 3 ，且 3 ^ 1 = 2 。所以第二个查询的答案为 [2,3] 。

推导：val ^ firsti == secondi => val ^ firsti ^ firsti = secondi ^ firsti=> val = secondi ^ firsti

技巧：x = x << 1 | (s[r] & 1); 把字符串中所有的二进制数取出来作为key，起始和终点作为value，存储在map中，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    vector<vector<int>> substringXorQueries(string s, vector<vector<int>>& queries) {
        unordered_map<int, pair<int, int>>mp;
        if(auto i = s.find('0'); i != string::npos) {
            mp[0] = {i, i};
        }
        // 预处理s中所有的二进制数, 如"101101",mp[1] = {l, r}, mp[101] , mp[1011], mp[10110], mp[101101]
        for(int l = 0; l < s.size(); l++) {
            if(s[l] == '0') {
                continue;
            }
            for(int r = l,  x = 0; r < s.size() && r < l + 30; r++) {
                x = x << 1 | (s[r] & 1); 
                auto it = mp.find(x);
                if(it == mp.end()) {
                    mp[x] = {l,r};
                }
            }
        }

        vector<vector<int>>ans;
        for(auto q : queries) {
            auto it = mp.find(q[0] ^ q[1]);
            if(it == mp.end()) {
                ans.push_back({-1, -1});
            } else {
                ans.push_back({it->second.first, it->second.second});
            }
        }
        return ans;
    }
};

（最近学习go，贴一版go） 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
func substringXorQueries(s string, queries [][]int) [][]int {
	type pair struct {
		l, r int
	}
	m := map[int]pair{} // key:int, value:pair
	if i := strings.IndexByte(s, '0'); i >= 0 {
		m[0] = pair{i, i}
	}
	// 预处理s中所有的二进制数 101101
	for l, c := range s {
		if c == '0' {
			continue
		}
		for r, x := l, 0; r < l+30 && r < len(s); r++ {
			x = x<<1 | int(s[r]&1) // x = 1，10，101，1011 。。。串起每个数字
			if p, ok := m[x]; !ok { //  p, ok := m[x]; !ok || l-r > p.r-p.l
				m[x] = pair{l, r}
			}
		}
	}

	ans := make([][]int, len(queries))
	notFound := []int{-1, -1}

	for i, q := range queries {
		p, ok := m[q[0]^q[1]]
		if ok {
			ans[i] = []int{p.l, p.r}
		} else {
			ans[i] = notFound
		}
	}
	return ans
}
FEATURED TAGS
字符串
FRIENDS